Explorations in Calculus
Calculus is the mathematics of change. In algebra and pre-calculus, students study relationships where one quantity changes relative to another, such as the position of a train leaving Chicago changing with time. By looking at where that train is at two different times, we can explore the idea of rate of change in position with respect to time. That idea is known to most of us as speed. In calculus, we take things a step further and notice that in many cases the rate of change is changing, or speed is variable. Isaac Newton is credited for much of the development of modern calculus, as he needed new mathematical strategies to explain just why that apple was not only falling, but falling faster the further it traveled.
![]() I know what you’re thinking: “Gross!” right?
I know what you’re thinking: “Gross!” right?
The word “calculus” seems to strike fear in the hearts of Algebra students, and understandably so. It is somewhat like learning a new language just to dissect the meaning of everything. Our definitions and notations incorporate the entire English alphabet and half of the Greek letters. P is different than p, which is different than p’, dp, pi, or p(x) or the Greek letter ρ that looks just like p, only rounder. On top of that, there are goofy new symbols and subscripts and not a complete sentence to be found.
But when the script can be translated, read aloud, and understood, calculus is an incredibly powerful tool for evaluating many very real and practical problems.
This semester, we don’t have an AP Calculus course. Our most advanced math student has been there, done that. So the analytical foundation has been set to explore applications to real-world problems. We are just wrapping up unit 1 in Multi-Variable Calculus, where we’ve explored numerous applications of integral calculus and discussed when and why it is appropriate to use these techniques to solve problems.
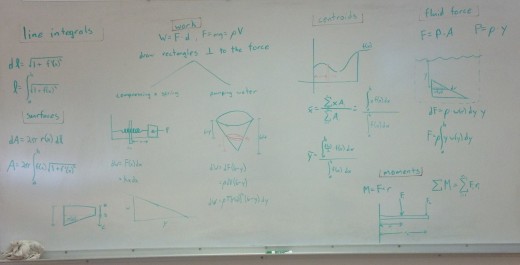
Among these topics, we are finding the length of lines to draw curves and the surface areas of bizarre curved shapes, such as vases. We look at the physics idea of “work” and study situation where forces or shapes are changing. We’ve learned strategies to find the center of mass for objects with curved edges and tapering thicknesses, such as kitchen knives. Lastly, knowing that water pressure is a function of depth, we’ve learned how to calculate the total force on a submarine porthole, an aquarium, or a parabolic turbine gate on Hoover Dam.
Study guide for the Applications of Integration unit
Students in every math classroom in the country ask: “when am I ever going to use this?”
At the Alzar School, we aim to answer that question every day.
-Dan Thurber, Alzar School Math Teacher