Just Something Random

The word “random” is one most people learn to misuse at an early age.  Teenagers and adults alike often use the word to refer to anything from an unexpected question to pickles on a grilled cheese sandwich.  Webster’s dictionary defines it as made, done, happening, or chosen without method or conscious decision.  “Random” questions are typically a product of thoughtful curiosity and “random” condiments are the product of them being delicious.  So the challenge was presented to our pre-calculus class last week: can you be truly “random?”

Basically, several students were instructed to cheat and cut corners on a coin toss lab.  They didn’t want to, but I made them cheat.  Just this once.  To actually do the lab, one must flip a coin lots of times and record the results.  Flip. Heads.  Flip. Heads. Flip. Tails.  And so forth for the next nine minutes of your life.  Booooorrrring!  Why not just hastily make up the results and then make a doodle of a whale with a mustache?  No one will know, right?

So while half of the students were diligently flipping coins to gather their data, others quickly came up with their own “random” list of coin tosses.  HTTHHTHHHTTTHTHHTTHHTHHTTHHTHTTHTHHTHHTHTHHT.  That was fast, now time to doodle.

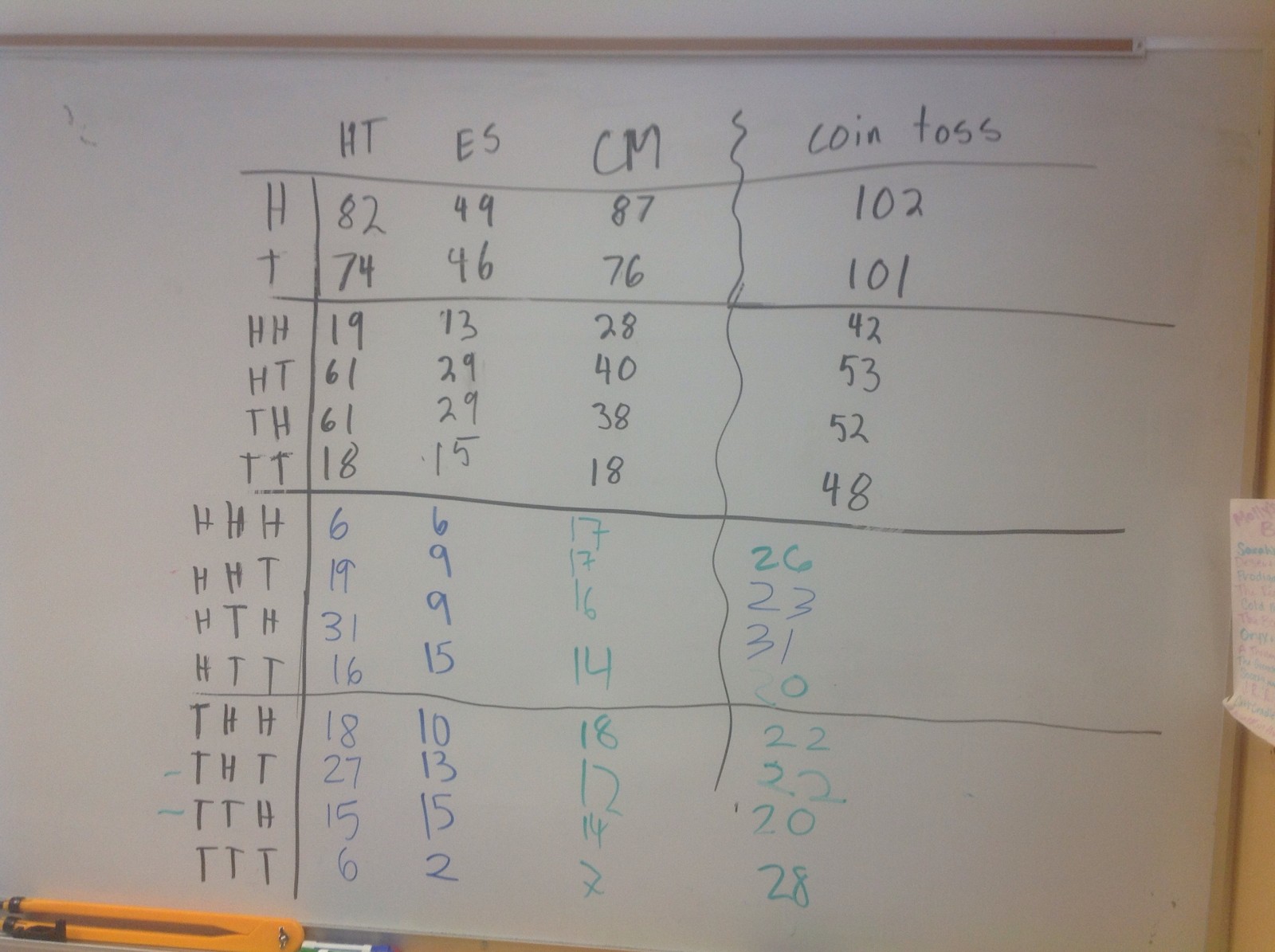
Nine exhausting minutes of coin tossing later, the results were in and ready for analysis.  How many heads and tails did each person get?  Those tossing coins compiled their data to even things out.  Here’s the tally with student initials across the top, outcomes of Heads or Tails labeled in the left-most column:

Okay, so the cheaters did alright.  There were a few more heads than tails, but you could certainly have gotten those same results experimentally.  If I was hunting for cheaters, the closeness of the coin toss almost seems too good to be true.  I’d be suspicious of them if anyone!

So now let’s look at patterns.  I’ll start with an easy probability question.  A coin is tossed, what is the probability it lands heads? 1/2 right?  Okay, it landed tails.  Sorry.  Let’s flip again.  What’s the probability of heads this time?  Do you think it’s still 1/2?  You’re absolutely right.  So in a perfect world, the occurrences of HT, HH, TH, and TT should all be equal.  Those are the four equally likely outcomes of a double flip.  Let’s see what happened when we tallied up consecutive toss outcomes for each data set:

The coin toss is close, with a few more cases of HT or TH than getting two in a row (HH or TT).  Meanwhile the students who made up their data have over twice as many alternating pairs as consecutive pairs!  Busted!

When we listed out all eight outcomes possible from three tosses, the results become even more distorted.  Our coin toss actually turned out HHH or TTT more commonly than most alternating possibilities.  Meanwhile, Emma and Hailey each chose perfect alternation at least FIVE TIMES more often than they chose three tails in a row.  They’re darn good students, but evidently lousy cheaters.

“Well, clearly people aren’t random because if you just chose heads, part of you wants to pick tails next to keep things even.  There’s a conscious decision.”  – Hailey T.

Subsequently, this spurred a class discussion about dependent vs. independent probability that quickly went down the road of when statistics actually relate to the conclusions based upon them and critical thinking.  I won’t get into that here, you’ll have to ask one of our pre-calc students.

-Dan Thurber