Mental math and the savvy traveler.

Good financial awareness is a mandatory skill for any successful foreign traveler.  There are many new considerations to address when you’re 4000 miles from the nearest US Bank branch and I certainly learned a lot from trial and error during my first big international trip.  To highlight the value of good quantitative reasoning skills while immersing in a new culture, the Alzar School Math and Spanish departments came together for a lesson on exchange rates before we took off for Chile.  We began by looking at prices of a few common goods in Chile, including a bus ticket, t-shirt, snickers bar, and 27″ TV.  Translating the listed price from Chilean Pesos (CHP) to US dollars (USD) proved quite easy when Google gave us an exchange rate of 1 USD = 473 CHP and we all had calculators in hand, but the goal is to understand the true cost of goods after all fees are accounted for.

The students set to work studying how cash exchange houses make their money, how ATM fees would impact them, whether they’re better off carrying US cash or making withdrawls at the “Cajero Automatico.”  What about paying directly with a credit card?  And most importantly, when a price says 6000 CHP for a t-shirt, is that a good deal?  How many liters of coke could I get for that, how many dollars are we talking here?  Learning to divide any number by 473 requires some serious mental math, and a certain level of acceptance for estimation and inaccuracy.  Either way, as we are two weeks in to our time in South America, it’s clear that everyone paid attention that day.  The students are making very appropriate price estimations and rational judgement of what is a good deal and when they’re getting the “gringo price.”  Mental math starts getting fun when the dollars are yours.

Which brings me to a new puzzler:  How many minutes are there in one year?  Sure, you could just sing the chorus of the song from RENT and know, but did you check your work?  This one came up as a mental math problem in the truck during the short shuttle drive back home from the Rio Enco.  It took Dezaray about 6 minutes to figure it out without a calculator.  Give it a shot!

Solution to the previous puzzler:

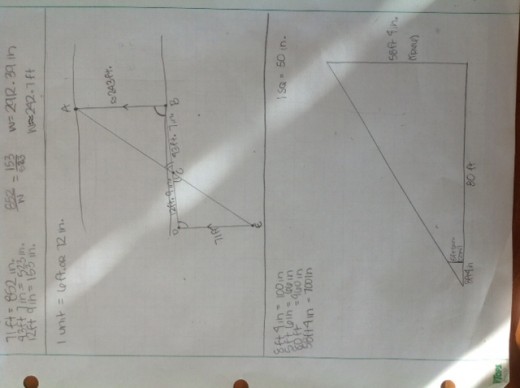
This is Roxy’s work with a scale drawing and similar triangles

As long as all lines are straight and AB is parallel to DE, the two triangles are similar and the width can be determined with a simple ratio.  Now I’ve taught the class about trigonometric ratios and they’re cursing me for making them do this exercise the hard way. 🙂

-Daniel Thurber, Alzar Math Department