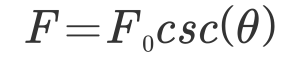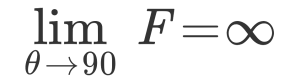Rescue class from a math teacher
Over the weekend of April 19th, I had the pleasure of teaching a fully-certified swiftwater rescue course to the Alzar students through the Swiftwater Safety Institute. Having worked so closely with these students throughout the semester, I had much more perspective of their abilities than I do for most weekend courses. For the students, taking the class from their math teacher meant they didn’t get a day off from academic thought and numerical precision. On the first day, I took it easy on math, just having the students compare breaking strengths of different materials and diameters of rope. They also had to know and use the conversion rate for kilonewtons to pounds if they wanted to know how their carabiners were rated.
On day two, we practice knots and anchors, which meant a more analytical look at breaking strength. Depending on the knot, a knot tied in a rope can reduce the rope strength by 25-50%. But doubling up a rope or using an anchor with multiple strands distributes the load and makes the system stronger. Furthermore, particular ratios of rope diameters need to be considered for certain multi-rope applications. Analyzing these systems got the students really thinking to identify the weak point. If you have a 5mm spectra cord tied in a prussic hitch around a 3/8″ polypropylene rope, with has a figure-8 knot attached to a two-bight anchor (made with a 1″ nylon webbing sling tied with a water knot) with a 31-kN aluminum carabiner, how strong is the connection? Where is the weak point?
The fun really took off when we studied the principles of mechanical advantage and pulley systems, angles, and mechanical advantage. A pulley attached to a fixed point merely changes the direction of the rope and reduces friction. But in doing so, it exerts double the force on the anchor.
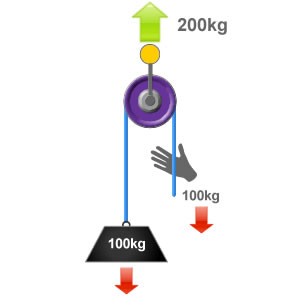
If we anchor the pulley in a moving part of the system, or to what we’re trying to move, we can get mechanical advantage to move heavy things (see 3:05).
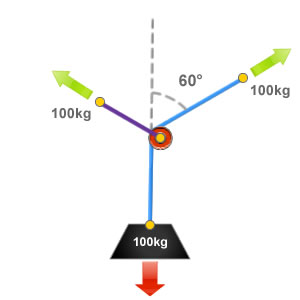
We also took a quick look at how angles in a system can affect the resultant loads and multiply force, and proved that if two anchor points are far enough apart to generate a 120-degree angle, the anchors are no longer distributing the force, but each supporting a full load:
Finally, we applied these principles to another type of mechanical advantage called a vector pull. The idea is to get a taughtrope to a pinned boat and pull on it in a perpendicular direction.
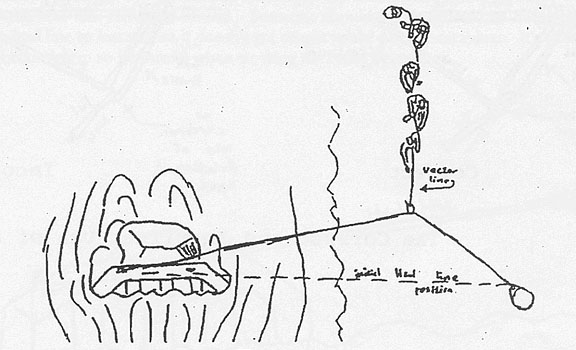
Textbook will say this gives “significant mechanical advantage,” but that doesn’t cut it in our quest for precision. We assigned the angle of displacement between the original rope position (dotted line) and the new rope position (solid line) to be given by θ, the input force on the vector line to be represented by Fο, and the resultant force represented by F. The forces and angles are related by the following equation.
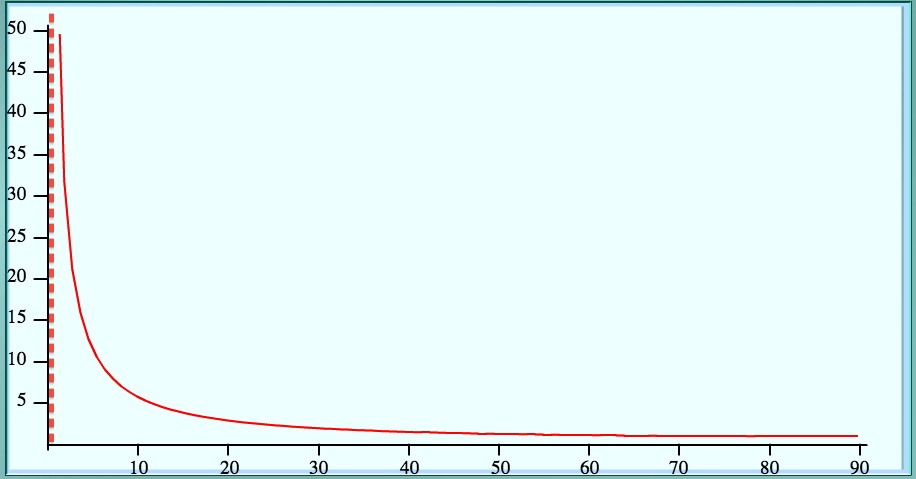
“Grace, you’re taking a trig test today. Come sketch the cosecant graph from 0° to 90° for us.”
“Ok, team, what’s the story on that dotted line?”
Darby from Algebra 2 pipes up: “It’s a vertical asymptote!”
“Which means what about the force as our angle decreases?”
Calculus students were already using their understanding of limits to describe the behavior of the force-angle relationship and say:
“So class, tying this all back to what we’re talking about this weekend, which is river rescue, what needs to happen for our vector pull to achieve mechanical advantage?”
Everyone got the point. The vector pull works better and better the smaller the angle is. Our rope must be as tight as possible before we pull perpendicular. The students will probably apply this understanding on a very regular basis. Hopefully it’s mostly to rig up great clotheslines after a day on the water.
-Dan Thurber, Alzar School Math Teacher