Solving math problems with several unknowns

The Algebra II class at the Alzar School has been working through some interesting problems with systems of equations.  A basic system of equations involves two equations that each relate two unknown quantities.  The system can be solved through techniques of substituting one equation into the other, combining equations to eliminate a variable, or graphing both equations and identifying where two lines intersect.

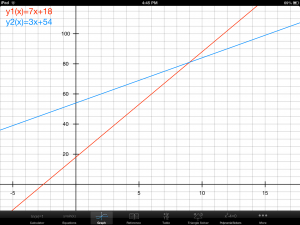
The unit on systems of equations lends itself to word problems.  For example: “A golf club offers two choices for a membership.  You can pay $18/month and pay an additional $7 each round, or buy a premium membership for $54/month and pay $3 per round.”  If we assign variables d=number of days you go golfing and C=the total monthly membership cost, the basic membership cost is modeled by C = 7d + 18.  Likewise, the second equation is modeled by C = 3d + 54.

Solving the system gives a result of C = $81 and d = 9 days, meaning that if you play 9 rounds of golf each month, both membership options cost the same.  More regular golfers will benefit from the premium membership and hobbyists such as myself should choose the basic option.

In Algebra II, we focus very heavily on translating written situations into mathematical equations that can be solved to determine unknown quantities.  These word problems often frustrate students at first, but demonstrate the important practical applications of the material we are learning.  For more advanced problems, we have gotten into systems with three variables and three equations.  The following word problem was a project the students toiled over during our Chilean paddling expedition:

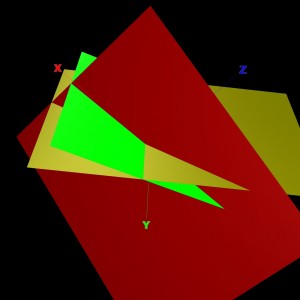
“A mixture of 12 liters of chemical A, 16 liters of chemical B, and 26 liters of chemical C is required to kill a destructive crop insect.  Commercial spray X contains 1, 2, and 2 parts, respectively, of each chemical.  Commercial spray Y contains only chemical C.  Commercial spray Z contains only chemicals A and B in equal amounts.  How much of each type of commercial spray is needed to get the desired mixture?”

This problems tests students’ ability to explicitly define variables, understand unknown quantities, and write algebraic expressions to represent the system.  The hardest part of this problem is writing out three different equations with three variables to create a system that can be solved.  The math is easy.  Take a shot at it; see if you can translate the situation into usable equations.

(Hint: x, y, and z are you unknowns, not A, B, and C.  A, B, and C are the equations you must write.)  This problem can also be solve by graphing.  The solution is the point where all three planes intersect in space!

-Dan Thurber, Math Teacher