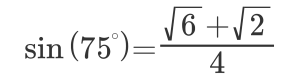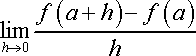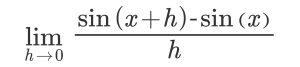When Will I Ever Use This?

In the math department at the Alzar School, I have now taught or mentored six years worth of High School curriculum, from Algebra I to Vector Calculus.  One nicety of this breadth has been an opportunity to see concepts that are learned in one class with apparent frivolity be applied in more advanced topics.  Most recently, I’ve been having quite a bit of fun exploring some uses of analytical trigonometry.

Our trig class is currently studying analytical trigonometry, which doesn’t really involve triangles, or the unit circle, but just explores relationships between the commonly known trigonometric ratios (sine, cosine, tangent) and the implications of those relationships.  For example, did you know that

or

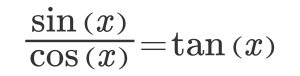
Always!  Every time!  Pick some numbers of your own and try it out!

More recently, we introduced something called a sum formula.  There are six of them, but here is the first.

Now, that may seem somewhat boring or intimidating or unnecessary.  One of the practice exercises where we apply this formula is to find the exact value of sin(75).  We can use special triangles to find exact values of sin(45), sin(30), and the cosines of each angle, but we can’t simply add those values.  We can, luckily, use the sum formula to help us and ultimately prove that

Ok, great.  So what?  Technically, this is an “exact” answer, compared to the “decimal approximation” of sin(75)=0.965926.  Any engineer, architect, or surveyor will be much more interested in the latter expression, leaving us feeling like the whole sum formula routine was nothing more than a neat trick.

Enter Calculus.  The foundation of calculus is the limit process and subsequently the derivative.  To find the derivative of a function, we enter the function rule into the definition of the derivative.  Any former calculus students out there ought to recognize this one:

When this definition of the derivative is applied to the sine function, we are left to evaluate the limit statement:

Can you see where I’m going with all this?  Do you see where our sum formula could be applied to rewrite this?  All family members who attended Parent’s Weekend this semester got to watch in awe as Derek expanded this statement, applied some properties of limits, and ultimately proved to us that:

Pre-Calculus is just that: a deeper exploration of algebra and an introduction to many of the analytical techniques that get used and applied in calculus.  It’s fairly unlikely that any current Alzar School student will find a career that has them evaluating derivatives on a daily basis.  Even engineers and statisticians leave most of the dirty work up to computer programs.  But statements, definitions and ultimately solutions should not be accepted by students simply because their math teacher or a computer said so.  These kinds of explorations serve an important purpose of showing students how we’ve gotten to where we are and how others have creatively problem-solved and used concrete evidence to support their claims.